Malekko/Wiard/Richter Noisering[modifier]
Block Diagram[modifier]
Documentation, ancien site Wiard, et Cybernetics expander[modifier]
=> Fichier:Cybernetics, noisering.pdf
Cybernetics, noisering entropy controler Expander[modifier]
Noisering Analysis by Babaluma[modifier]
Comparator
“In electronics, a comparator is a device which compares two voltages or currents and switches its output to indicate which is larger.”
The Noisering has two comparators: one to determine the Chance value and to determine the Change value. The output of a comparator is 0 or 1.
Shift register
“In digital circuits, a shift register is a cascade of flip flops, sharing the same clock, which has the output of any one but the last flip-flop connected to the "data" input of the next one in the chain, resulting in a circuit that shifts by one position the one-dimensional "bit array" stored in it, shifting in the data present at its input and shifting out the last bit in the array, when enabled to do so by a transition of the clock input.”
The Noisering has one 8-bit shift register. The state of the register is translated by two DACs into a voltage in the range of 0-10 volts. One DAC (output 1) provides 256 voltage values, the other (output 2) provides 9 voltage values. ‘00000000’ is the shift register state that represents 0V, ‘11111111’ is the shift register state that represents 10V.
The shift register ‘shifts bits’ at a rate determined by the Rate pot or at a rate determined by the clock input.
Chance
The Chance pot by default attenuates an internal DC voltage. You can also supply a voltage via the Chance input. In either case the Chance voltage is compared against the voltage of an internal analog noise source. If the Chance voltage is greater than the analog noise voltage, the Chance comparator output is 1. If the Chance voltage is smaller than the analog noise voltage, the Chance comparator output is 0.
This means the more clockwise you turn the Chance pot, the greater the Chance voltage, the greater the chance the output of the Chance comparator is 1. The output of the Chance comparator is used as a ‘new value’ for the shift register input.
Change
The Change comparator works exactly the same way: an internal DC voltage or a voltage supplied via the Change input is attenuated by the Change pot and this voltage gets compared to the analog noise voltage. The output of the Change comparator determines if the shift register input gets a ‘new value’ (Change comparator output is 1), or an ‘old value’ (Change comparator output is 0).
A ‘new value’ is the output of the Chance comparator. An ‘old value’ is the last bit from the shift register. This bit gets recycled so to speak.
In practice this means that when the Change pot is turned fully counter clockwise, the input of the shift register only gets values from the last bit. This results in a repeating pattern in the shift register. If you monitor one of the DAC outputs at audio rate you will here a steady tuned tone.
The more clockwise you turn the Change pot, the more new values will arrive at shift register input, which leads to ever more changing patterns in the shift register.
Another worthy thing to note: the more the shift register is occupied by zeros, the greater the chance the DACs output a low voltage (‘00000000’ represents 0V). And of course the more the shift register is occupied by ones, the greater the chance the DACs output a high voltage.
WIARD Information from muff forum[modifier]
WIARD INFORMATION
NOISE RING INFO:
I am wondering if can anyone explain the relationship between the "Ring" lights and the bits flowing through the shift register. It seems that higher voltages are present when the LEDs are red, but I can't quite understand how the three states (green, red, off) relate to the two states (one, zero) of the shift register.
the shift register is an 8-bit register divided into two four-bit 'nibbles'.
the first nibble is: do d1 d2 d3 and the second is d4 d5 d6 d7
the 4 leds indicate a comparison between the states of the following pairs of bits: d0 - d4 d1 - d5 d2 - d6 d3 - d7
using d0-d4 as an example: when d0 = d4 led is OFF when d0 > d4 led is green when d0 < d4 led is red (I might have the green/red states reversed)
My assumption regarding why Grant used this method is that it is a good indicator of CHANGE - which is the exact type of feedback the user needs to adjust probablility controls. The compromise is of course that it is very hard to determine the exact state of the 8-bit register from this 4-led display. But (i likewise assume) devoting an entire 8-led subassembly and the requisite panel real estate for a direct register display would have been more costly. The 'Goldberg jr.' that i gave Grant in July 2001 had an 8-led direct display but no clock or data indicators. I'm impressed with the efficiency and economy of the scheme Grant devised to get a lot of feed back to the user with just 8 lights and very low current consumption. Hope this helps you 'read' what your marvelous little gadget is doing.
I am having a hard time getting the noise ring to process external data. In particular, I have been unable to achieve the phased sound when patching another oscillator into the chance input jack. When I do this and monitor the main out I hear nothing at all. Has anyone else had this problem? What could I be doing wrong?
1. Make sure the "Change" pot is all the way up (LED full on). 2. Input a VCO 10 volt peak to peak triangle or sawtooth wave into "Chance In" jack. 3. Adjust "Chance" control so some LED signal is seen. 4. Monitor main output and play with VCO frequency and "Rate" setting.
Run an external audio signal of +/- 5 volts into the "Chance In" input jack. This is normalled to the white noise output.
Set the "Change" knob all the way on. Vary the "Chance" control knob to change the sound.
Also vary the "Rate" knob to change the sound. You can reduce the setting of the "Change" control knob as an experiment.
In order to avoid re-inventing the wheel, please read the circuit desciption Grant posted at:
http://www.wiard.com/1200/NR/Noise_Ring.html
=> Fichier:Cybernetics, noisering.pdf
i will be referring to the block diagram he posted.
regarding digital noise: If we force a feature-by-feature comparison of the I.D. and the N.R, the one feature that the N.R. lacks is a 'conventional' digital noise source. The main and aux outputs of the N.R. are both digital noise , to be sure, but they are both variable in spectrum and controlled by the two CV vectors, "Change' & Chance'. This makes them a little different from conventionally produced digital noise sources (such as the now extinct MM5x37 chips).
The Blacet I.D. is a very full featured implementation of a tried and true, time-honored method of random voltage generation in analog modulars. To wit, a noise source (continuously variable between digital or analog) is 'snapshotted' by a sample hold at a voltage controlled sample rate and output as random steps. The pattern of these steps vary in amplitude according to the spectrum of the input noise and , in duration by the clock rate. Thus, the output steps are derived dirctly from the noise sources, analog , digital or some mix of both.
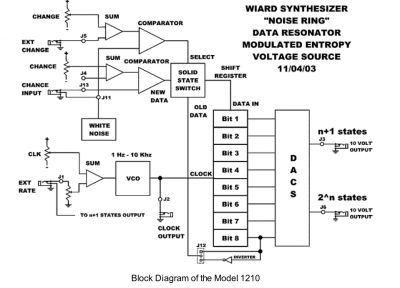
The Wiard N.R. uses analog noise at a basic source point in it's algorithm, but never directly. This noise is never sampled by an sample/hold circuit, in fact there are no sample/hold circuits in the N.R and this is a fundamental distinction. (It will help to consult the N.R. block diagram, at this point) You may already know how a shift register works but for anyone who doesn't, i'm going to use the analogy of a conveyer belt with room for 8 people....
In the N.R., analog noise is used to tickle the threshold of a comparator, the comparator flips on and off producing either 'someone' or 'no one'. depending on the state of the comparator. This person/non-person stands OFF the conveyer belt waiting for a signal. The signal comes from the clock. The clock is also a 2-state device. We'll call them 'tick' and 'tock'. Remember that the clock is not steady. It varies with a CV. This is important. When the clock is in a 'tock' state , nothing happens. The conveyer belt doesn't move and no one steps on. The N.R.'s output is static. But when the clock switches to "tick" the conveyer belt moves one step and if the comparator was tickled to it's 'someone' state, someone steps aboard. If it was in 'no one' state the conveyer moves one step with an empty place. On the next tick the conveyer lurches forward and if anyone was in the last (8th) position they get dumped off. Another thing happens at each tick, the DAC takes a snapshot of the pattern of occupied and unoccupied places on the conveyer, and based on that pattern it sends a voltage to the output, a different voltage for every different pattern, Thus as the two devices, comparator and clock, go on flickering , the conveyer gets loaded with different patterns that SHIFT on each tick. This cycling of patterns is the heart of the N.R.'s method, and this is very close to the classic function of a digital shift register.
But there are some twists! And one of the more brilliant twists that Grant conceived is depicted in the block digram by the line marked 'old data' feeding the "solid state switch' . This is controlled by the 'Change' control. As the 'Change' control vector decreases, the chances INCREASE that the passenger who was just dumped off the end of the conveyer will get another turn and move right back to the front of the conveyer again and prevents any 'new' passengers (from the flickering comparator) from boarding. The effect of this is a 'circular' buffer wherein the pattern repeats ad infinitum until 'new' passengers are re-introduced by increasing the change control. At slow clock rates this results in cycling patterns. At audio clock rates the effect is a clearly discernible pitch. The wonderful thing about this is that the change control vector is continuous and thus, at audio frequencies, random audio (noise) will start to organize itself into a pitched tone. The 'between states' are sublime (to my perverse ear, anyway) and if you descend into chaos again , when you morph to pitch the next time there's no guarantee that you'll get the same wave as before. Please forgive me for editorializing, but the resulting patterns are exquisite!!! i'm sorry to confess my fetish, but that's just the very definition of my personal idea of a good time!
To drag this screed back to the issue of comparison. The method of pattern generation just described is very different than the sample/hold method used by the I.D. (and MANY other RVG is modular synth history). Most importantly, this method yields a very different character of output patterns than a sample/hold-based design produces. The noise sources are never sampled directly and thus, the output SOUNDS different from sample/hold-based output. i've foolishly engaged in past disputes about whether this is can be called 'random' or not, and if it IS randow, how random is it? That's a semantic issue and a waste of time. The bottom line is that the noise ring yields MUSICALLY interesting patterns (to my ear) and that's what matters. In all fairness, Sample/holds yield interesting patterns too (i have 9 versions of them, at last count) but the noise ring's output is distinct from all of them. The other very important distinction is the effect of the ability to exercise a very fine level of control over the 'chance' and 'change' parameters. This is a unique and VERY powerful feature.
The Buchla "Sources of Uncertainty' is the seminal circuit that employs a similar use of noise (as a modulator of the sampled source, rather than the noise being the sampled source itself), and a recursive structure that can create suprisngly musical patterns in the name of UNCERTAINTY, which I think is a better term than RANDOMNESS.
When I use the term entropy I mean Shannon's measure of information entropy, not thermodynamic entropy (which uses a similar equation, the reason Shannon used the term "entropy"). Information entropy is just a histogram of the number of levels in a matrix of information, expressed as the number of bits needed to store that number of levels. If there are only two levels, you only need 1 bit to store it. If there are 4 levels, you need 2 bits to store the information and so on.
The original Buchla 266 presented control of the level entropy of the uncertainty source (from 1 to 6 bits). But there was no control over the frequency spectrum entropy (if you calculated the information entropy of the DFT). The Buchla 265 sample and hold presented control of the time spectrum entropy via the recursion control, but not the level entropy.
The Noise Ring provides both types of control, level entropy via the "Chance" control, and frequency spectrum entropy via the "Change" control.
I don't know if this is scientifically true, but it is believeable that the ear does both types of entropy measurements at a very fundimental level. The ear uses a kind of "battery" system to supply the ear, because blood flow would be too noisy. The ear uses "hairs" to sense both level and frequency information. IF an excited cell uses more "current" than a non-excited one, then the way the ear is structured, the information entropy is proportional to the "current draw" for the two different "hair" structures. One for levels (amplifier cells) and one for time spectrum entropy (cochlial cells). Higher information entropy excites more cells, which draw more "current".
Grant Richter, from Muff[modifier]
The Noise Ring is inspired by an Electronotes design called a "PERTWEE" or "Pseudo Random Tone Wheel" which is in EN#106. that design uses a pseudo random shift register as the noise source and pieces of the pseudo random sequence are grabbed by a "tone wheel" and recirculated. The design uses an enormous number of parts. The probability of change control uses 32 comparators and gates for example.
The Noise Ring uses an actual noise source with comparators to control the grabbing of data (CHANCE) into the wheel and the recirculation of data (CHANGE).
Now if the wheel had all zeros in it, or all ones, it would make no sound, so there is a circuit to detect these conditions and force a single zero or single one into the wheel so it always makes a tone.
This is why when "CHANCE" is at either extreme, there is still a tone coming out.
The wheel output bits are connected to two DACs similar to the Buchla 266 so output #1 produces "N+1" or 9 levels and output #2 produces "2^N" levels or 256. Output #2 is shown on the red led. Output #1 is feedback to "Ext. Rate" to produce simpler more melodic patterns.